WikiDer > Куб
| Правильный шестигранник | |
|---|---|
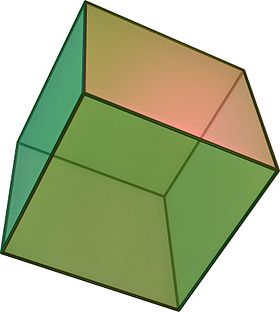 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Платоново твердое тело |
| Элементы | F = 6, E = 12 V = 8 (χ = 2) |
| Лица по сторонам | 6{4} |
| Обозначение Конвея | C |
| Символы Шлефли | {4,3} |
| t {2,4} или {4} × {} tr {2,2} или {} × {} × {} | |
| Конфигурация лица | V3.3.3.3 |
| Символ Wythoff | 3 | 2 4 |
| Диаграмма Кокстера | |
| Симметрия | Очас, B3, [4,3], (*432) |
| Группа вращения | О, [4,3]+, (432) |
| Рекомендации | U06, C18, W3 |
| Характеристики | обычный, выпуклыйзоноэдр |
| Двугранный угол | 90° |
 4.4.4 (Фигура вершины) |  Октаэдр (двойственный многогранник) |
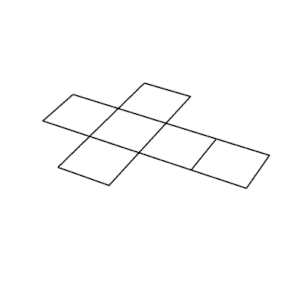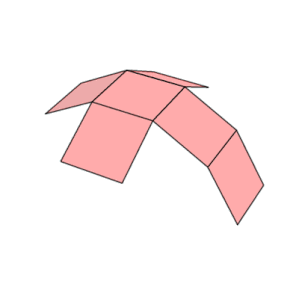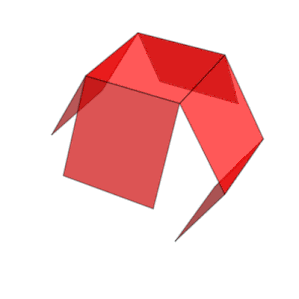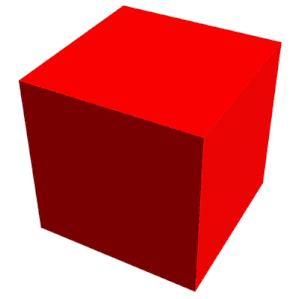
 Сеть | |
В геометрия, а куб[1] это трехмерный твердый объект, ограниченный шестью квадрат лица грани или сторон, по три встречи на каждой вершина.
Куб - единственный обычный шестигранник и является одним из пяти Платоновы тела. У него 6 граней, 12 ребер и 8 вершин.
Куб - это тоже квадрат параллелепипед, равносторонний кубовид и право ромбоэдр. Это правильный квадрат призма в трех ориентациях, а треугольный трапецоэдр в четырех направлениях.
Куб это двойной к октаэдр. Имеет кубическую или октаэдрическая симметрия.
Куб - единственный выпуклый многогранник, все грани которого равны квадраты.
Ортогональные проекции
В куб имеет четыре специальных ортогональные проекциипо центру, на вершине, ребрах, грани и нормали к ее вершина фигуры. Первый и третий соответствуют A2 и B2 Самолеты Кокстера.
| В центре | Лицо | Вершина |
|---|---|---|
| Самолеты Кокстера | B2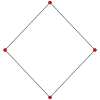 | А2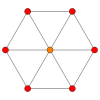 |
| Проективный симметрия | [4] | [6] |
| Наклонные взгляды |  |  |
Сферическая черепица
Куб также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
 |  |
| Ортографическая проекция | Стереографическая проекция |
|---|
Декартовы координаты
Для куба с центром в начале координат, с ребрами, параллельными осям, и с длиной ребра 2, Декартовы координаты вершин
- (±1, ±1, ±1)
а интерьер состоит из всех точек (Икс0, Икс1, Икс2) с −1 < Икся <1 для всех я.
Уравнение в
В аналитическая геометрия, поверхность куба с центром (Икс0, у0, z0) и длина кромки 2а это локус всех точек (Икс, у, z) такие, что
Куб также можно рассматривать как предельный случай трехмерного суперэллипсоид поскольку все три показателя стремятся к бесконечности.
Формулы
Для куба с длиной ребра :
| площадь поверхности | объем | ||
| диагональ лица | диагональ пространства | ||
| радиус ограниченная сфера | радиус касательной к краям сферы | ||
| радиус вписанная сфера | углы между лицами (в радианы) |
Поскольку объем куба - это третья степень его сторон , третьи силы называются кубики, по аналогии с квадраты и вторые силы.
Куб имеет самый большой объем среди кубоиды (прямоугольные коробки) с заданным площадь поверхности. Кроме того, куб имеет самый большой объем среди кубоидов с таким же общим линейным размером (длина + ширина + высота).
Точка в пространстве
Для куба, описывающая сфера которого имеет радиус р, а для данной точки в ее трехмерном пространстве с расстояниями dя из восьми вершин куба имеем:[2]
Удвоение куба
Удвоение куба, или Делианская проблема, была проблема древнегреческие математики использования только компас и линейка чтобы начать с длины ребра данного куба и построить длину ребра куба с удвоенным объемом исходного куба. Решить эту задачу им не удалось, и в 1837 г. Пьер Ванцель оказалось невозможным, потому что кубический корень из 2 не является конструктивное число.
Равномерная окраска и симметрия

Куб имеет три одинаковых раскраски, названных цветами квадратных граней вокруг каждой вершины: 111, 112, 123.
Куб имеет четыре класса симметрии, которые могут быть представлены как вершинно-транзитивный раскрашивание лиц. Высшая октаэдрическая симметрия Oчас все лица одного цвета. В двугранная симметрия D4ч происходит от куба, представляющего собой призму, все четыре стороны которой одного цвета. Призматические подмножества D2d имеет ту же раскраску, что и предыдущий, а D2ч имеет чередующиеся цвета сторон, всего три цвета, соединенные противоположными сторонами. Каждая форма симметрии имеет разные Символ Wythoff.
| Имя | Обычный шестигранник | Квадратная призма | Прямоугольный трапеция | Прямоугольный кубовид | Ромбический призма | Тригональный трапецоэдр |
|---|---|---|---|---|---|---|
| Coxeter диаграмма | ||||||
| Schläfli символ | {4,3} | {4}×{ } rr {4,2} | s2{2,4} | { }3 tr {2,2} | { }×2{ } | |
| Wythoff символ | 3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
| Симметрия | Очас [4,3] (*432) | D4ч [4,2] (*422) | D2d [4,2+] (2*2) | D2ч [2,2] (*222) | D3D [6,2+] (2*3) | |
| Симметрия порядок | 24 | 16 | 8 | 8 | 12 | |
| Изображение (униформа окраска) |  (111) |  (112) |  (112) |  (123) |  (112) |  (111), (112) |
Геометрические отношения

В кубе одиннадцать сети (один показан выше): то есть существует одиннадцать способов сгладить полый куб, разрезав семь граней.[3] Чтобы раскрасить куб так, чтобы никакие две смежные грани не имели одинаковый цвет, потребуется как минимум три цвета.
Куб - это ячейка единственная регулярная мозаика трехмерного евклидова пространства. Он также уникален среди Платоновых тел тем, что имеет грани с четным числом сторон, и, следовательно, это единственный член этой группы, который является зоноэдр (каждая грань имеет точечную симметрию).
Куб можно разрезать на шесть одинаковых квадратные пирамиды. Если эти квадратные пирамиды затем прикрепить к граням второго куба, ромбический додекаэдр получается (пары копланарных треугольников объединены в ромбические грани).
Другие размеры
Аналог куба в четырехмерном Евклидово пространство имеет особое имя - а тессеракт или же гиперкуб. Вернее, гиперкуб (или п-мерный куб или просто п-куб) является аналогом куба в п-мерное евклидово пространство и тессеракт - это гиперкуб порядка 4. Гиперкуб также называют мерный многогранник.
Есть аналоги куба и в более низких измерениях: точка в размерности 0, a отрезок в одном измерении и квадрат в двух измерениях.
Связанные многогранники

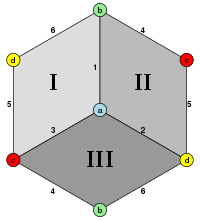
Частное куба на противоположный карта дает проективный многогранник, то гемикуб.
Если исходный куб имеет длину ребра 1, его двойственный многогранник (ан октаэдр) имеет длину ребра .
Куб является частным случаем в различных классах общих многогранников:
| Имя | Равные длины кромок? | Равные углы? | Прямые углы? |
|---|---|---|---|
| Куб | да | да | да |
| Ромбоэдр | да | да | Нет |
| Кубоид | Нет | да | да |
| Параллелепипед | Нет | да | Нет |
| четырехсторонний граненый шестигранник | Нет | Нет | Нет |
Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр; в более общем смысле это называется полукуб. Эти двое вместе образуют обычный сложный, то Stella Octangula. Их пересечение образует правильный октаэдр. Симметрии правильного тетраэдра соответствуют симметрии куба, который отображает каждый тетраэдр в себя; другие симметрии куба отображают их друг в друга.
Один такой правильный тетраэдр имеет объем 1/3 этого куба. Оставшееся пространство состоит из четырех равных неправильных тетраэдров объемом 1/6 куба каждый.
В исправленный куб это кубооктаэдр. Если срезать меньшие углы, получится многогранник с шестью восьмиугольный лиц и восемь треугольных. В частности, мы можем получить правильные восьмиугольники (усеченный куб). В ромбокубооктаэдр получается путем обрезания углов и краев до нужной длины.
Куб можно вписать в додекаэдр так что каждая вершина куба является вершиной додекаэдра, а каждое ребро - диагональю одной из граней додекаэдра; взятие всех таких кубиков дает правильное соединение из пяти кубиков.
Если два противоположных угла куба усечь на глубине трех вершин, непосредственно связанных с ними, получается неправильный октаэдр. Восемь из этих неправильных октаэдров могут быть присоединены к треугольным граням правильного октаэдра, чтобы получить кубооктаэдр.
Куб топологически связан с серией сферических многогранников и мозаик третьего порядка. фигуры вершин.
| *п32 изменения симметрии правильных мозаик: {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
Кубооктаэдр - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {31,1} | т {3,4} т {31,1} | {3,4} {31,1} | рр {4,3} s2{3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | час2{4,3} т {3,3} | с {3,4} с {31,1} |
= | = | = | ||||||||
| Двойники к однородным многогранникам | ||||||||||
| V43 | V3.82 | V (3,4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Куб топологически связан как часть последовательности правильных мозаик, простирающейся в гиперболическая плоскость: {4, p}, p = 3,4,5 ...
| *п42 мутации симметрии правильных мозаик: {4,п} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактный гиперболический | Паракомпакт | ||||||||
 {4,3} |  {4,4} |  {4,5} |  {4,6} |  {4,7} |  {4,8}... |  {4,∞} | |||||
С двугранная симметрия, Ди4, куб топологически связан серией однородных многогранников и мозаик 4.2n.2n, простирающихся в гиперболическую плоскость:
| *п42 мутации симметрии усеченных мозаик: 4,2п.2п | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Усеченный цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| н-кис цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
Все эти цифры имеют октаэдрическая симметрия.
Куб является частью последовательности ромбических многогранников и мозаик с [п,3] Группа Коксетера симметрия. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты.
| Мутации симметрии двойственных квазирегулярных мозаик: V (3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидово | Гиперболический | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Плитка |  |  |  |  |  |  |  | ||||
| Конф. | В (3,3)2 | V (3,4)2 | В (3,5)2 | В (3,6)2 | В (3,7)2 | V (3.8)2 | V (3.∞)2 | ||||
Куб - это квадратная призма:
| Семья униформы призмы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Многогранник | |||||||||||
| Coxeter | |||||||||||
| Плитка | |||||||||||
| Конфиг. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 |
Как треугольный трапецоэдр, куб относится к семейству гексагональной диэдральной симметрии.
| Однородные шестиугольные двугранные сферические многогранники | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
| {6,2} | т {6,2} | г {6,2} | т {2,6} | {2,6} | rr {6,2} | tr {6,2} | sr {6,2} | с {2,6} | ||||||
| Двойники к униформе | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
 Соединение трех кубиков |  Соединение пяти кубиков |
В однородных сотах и полихорах
Это элемент 9 из 28 выпуклые однородные соты:
Это также элемент пяти четырехмерных однородная полихора:
| Тессеракт | Собранный 16-элементный | Бегущий тессеракт | Cantitruncated 16-элементный | Усеченный 16-элементный |
 |  |  |  |  |
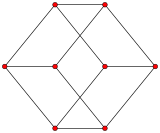
Кубический граф
| Кубический граф | |
|---|---|
 | |
| Названный в честь | Q3 |
| Вершины | 8 |
| Края | 12 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 4 |
| Автоморфизмы | 48 |
| Хроматическое число | 2 |
| Характеристики | Гамильтониан, обычный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф |
| Таблица графиков и параметров | |
В скелет куба (вершины и ребра) образуют график, с 8 вершинами и 12 ребрами. Это частный случай граф гиперкуба.[4] Это один из 5 Платоновы графики, каждый - скелет своего Платоново твердое тело.
Расширение - трехмерное k-ари Граф Хэмминга, который для k = 2 - куб-граф. Подобные графы встречаются в теории параллельная обработка в компьютерах.
Смотрите также
Рекомендации
- ^ английский куб со старофранцузского <латинского куб <Греческий κύβος (Кубос) означает «куб, кубик, позвонок». В свою очередь от ПИРОГ * кеу (б) -, "гнуть, повернуть".
- ^ Парк, Пу-Сун. "Расстояния регулярных многогранников", Форум Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf В архиве 2016-10-10 на Wayback Machine
- ^ Вайсштейн, Эрик В. "Куб". MathWorld.
- ^ Вайсштейн, Эрик В. «Кубический график». MathWorld.
внешняя ссылка
- Вайсштейн, Эрик В. "Куб". MathWorld.
- Куб: интерактивная модель многогранника*
- Объем куба, с интерактивной анимацией
- Куб (Сайт Роберта Уэбба)